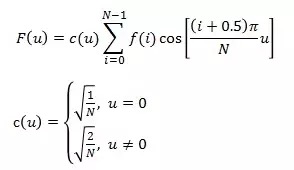个人博客

0%

001-感知哈希算法

发表于 更新于 分类于

摘要：001-感知哈希算法

两个图片是否是同一个图片内容

绝对一样【数据存储结构一样】

如果就是复制出来的，其实比较两个图片的 普通 sha 或者md5即可，

此处比对的是文件的数据结构。

相似图片

如果两个图片内容一样，但是有的经过压缩处理了，大小不一样，即存储结果不一样

感知哈希

感知哈希算法（Perceptual hash algorithm），是一类哈希算法的总称，它的作用是对每张图片生成一个”指纹”（fingerprint）字符串，比较不同图像的指纹信息来判断图像的相似性。结果越接近图像越相似。

感知哈希算法包括均值哈希（aHash）、感知哈希（pHash）和dHash（差异值哈希）。

aHash速度较快，但精确度较低；pHash则反其道而行之，精确度较高但速度较慢；dHash兼顾二者，精确度较高且速度较快。

在得到64位hash值后，使用汉明距离量化两张图像的相似性。汉明距离越大，图像的相似度越小，汉明距离越小，图像的相似度越大。

汉明距离

汉明距离是使用在数据传输差错控制编码里面的，汉明距离是一个概念，它表示两个（相同长度）字对应位不同的数量，我们以d（x,y）表示两个字x,y之间的汉明距离。对两个字符串进行异或运算，并统计结果为1的个数，那么这个数就是汉明距离。例如：
1011101与1001001之间的汉明距离是2。
2143896与2233796之间的汉明距离是3。
“toned”与”roses”之间的汉明距离是3。

均值哈希（aHash）

  • a) 缩放图片：为了保留图像的结构，降低图像的信息量，需要去掉细节、大小和横纵比的差异，建议把图片统一缩放到8*8，共64个像素的图片；
  • b) 转化为灰度图：把缩放后的图片转化为256阶的灰度图；

灰度图相关算法（R = red， G = green， B = blue）
对于彩色转灰度，其基础的心理学公式为： Gray = R0.299 + G0.587 + B0.114，部分变种也很流行：
i. 浮点算法：Gray=R0.3+G0.59+B0.11
ii. 整数方法：Gray=(R30+G59+B11)/100
iii. 移位方法：Gray =(R76+G151+B28)>>8;
iv. 平均值法：Gray=（R+G+B）/3;
v. 仅取绿色：Gray=G；

  • c) 计算平均值： 计算进行灰度处理后图片的所有像素点的平均值；
  • d) 比较像素灰度值：遍历灰度图片每一个像素，如果大于平均值记录为1，否则为0；
  • e) 构造hash值：组合64个bit位生成hash值，顺序随意但前后保持一致性即可；
  • f) 对比指纹：计算两幅图片的指纹，计算汉明距离。

感知哈希（pHash）

感知哈希算法可以获得更精确的结果，它采用的是DCT（离散余弦变换）来降低频率。

  • a) 缩小尺寸
    为了简化了DCT的计算，pHash以小图片开始（建议图片大于8x8，32x32）。
  • b) 简化色彩
    与aHash相同，需要将图片转化成灰度图像，进一步简化计算量（具体算法见aHash算法步骤）。
  • c) 计算DCT
    DCT是把图片分解频率聚集和梯状形。这里以32x32的图片为例。

DCT变换的全称是离散余弦变换(Discrete Cosine Transform)，主要用于将数据或图像的压缩，能够将空域的信号转换到频域上，具有良好的去相关性的性能。DCT变换本身是无损的，但是在图像编码等领域给接下来的量化、哈弗曼编码等创造了很好的条件，同时，由于DCT变换时对称的，所以，我们可以在量化编码后利用DCT反变换，在接收端恢复原始的图像信息。对原始图像进行离散余弦变换，变换后DCT系数能量主要集中在左上角，其余大部分系数接近于零，DCT具有适用于图像压缩的特性。将变换后的DCT系数进行门限操作，将小于一定值得系数归零，这就是图像压缩中的量化过程，然后进行逆DCT运算，可以得到压缩后的图像。

离散余弦变换的原理：
一维DCT变换：

其中，f(i)为原始的信号，F(u)是DCT变换后的系数，N为原始信号的点数，c(u)可以认为是一个补偿系数，可以使DCT变换矩阵为正交矩阵。
二维离散余弦变换的正变换公式为：

  • d) 缩小DCT
    DCT的结果为32x32大小的矩阵，但只需保留左上角的8x8的矩阵，这部分呈现了图片中的最低频率。
  • e) 计算平均值
    如同均值哈希一样，计算DCT的均值
  • f) 进一步减小DCT
    根据8x8的DCT矩阵进行比较，大于等于DCT均值的设为”1”，小于DCT均值的设为“0”。图片的整体结构保持不变的情况下，hash结果值不变。
  • g) 构造hash值
    组合64个bit位生成hash值，顺序随意但前后保持一致性即可。
  • h）对比指纹：计算两幅图片的指纹，计算汉明距离。

差异值哈希（dHash）

相比pHash，dHash的速度更快，相比aHash，dHash在效率几乎相同的情况下的效果要更好，它是基于渐变实现的。

  • a) 缩小图片：收缩至9*8的大小，它有72的像素点；
  • b) 转化为灰度图：把缩放后的图片转化为256阶的灰度图。（具体算法见aHash算法步骤）；
  • c) 计算差异值：计算相邻像素间的差异值，这样每行9个像素之间产生了8个不同的差异，一共8行，则产生了64个差异值；
  • d) 比较差异值：如果前一个像素的颜色强度大于第二个像素，那么差异值就设置为“1”，如果不大于第二个像素，就设置“0”。
  • e) 构造hash值：组合64个bit位生成hash值，顺序随意但前后保持一致性即可。
  • f) 对比指纹：计算两幅图片的指纹，计算汉明距离。

小波哈希（wavelet hashing）

离散小波变换（DWT）是频表示的另一种形式。流行的DCT和傅立叶变换使用余弦函数作为sin\cos的基础：sin(x)，sin(2x)，sin(3x)等等。与此相反，DWT使用一个单一的功能作为基础，但在不同的形式：缩放和移动。基础功能是可以改变的，这就是为什么我们可以有Haar小波，Daubechie-4小波等，这尺度效应给我们很大“时频表示”的时候，低频部分类似于原始信号。

对比

aHash：平均值哈希。速度比较快，但是常常不太精确
pHash：感知哈希。精确度比较高，但是速度方面较差一些
dHash：差异值哈希。精确度较高，且速度也非常快。

使用

工具

代码地址

githubhttps://github.com/JohannesBuchner/imagehash

本地使用

1
pip install imagehash

安装后在：/Users/lihongxu6/opt/anaconda3/lib/python3.7/site-packages

代码使用：

1
2
3
4
5
6
7
8
9
10
11
12
>>> from PIL import Image
>>> import imagehash
>>> hash = imagehash.average_hash(Image.open('test.png'))
>>> print(hash)
d879f8f89b1bbf
>>> otherhash = imagehash.average_hash(Image.open('other.bmp'))
>>> print(otherhash)
ffff3720200ffff
>>> print(hash == otherhash)
False
>>> print(hash - otherhash)
36

使用示例

average hashing

平均散列，对于每个像素输出1，如果该像素是大于或等于平均值，否则为0。

主函数：
average_hash(image, hash_size=8)

案例：

1
2
3
4
5
6
7
8
9
10
11
12
hash_size = 6
hash1 = imagehash.average_hash(Image.open('1_1.jpg'),hash_size=hash_size)
print(hash1)
# > 354adab5054af0b7

hash2 = imagehash.average_hash(Image.open('5_1.jpg'),hash_size=hash_size)
print(hash2)
# > 5b7724c8bb364551

1 - (hash1 - hash2)/len(hash1.hash)**2 # 相似性
# 或
hash1 - hash2

perception hashing

感知哈希，不同于aHash，但首先它确实是离散余弦变换和频域。

主函数：
def phash(image, hash_size=8, highfreq_factor=4):

两个参数，一起决定了图片resize的大小，最适合的才最好，按照公式：

  • img_size = hash_size * highfreq_factor
  • hash_size代表最终返回hash数值长度
  • highfreq_factor，代表resize的尺度
    案例：
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    highfreq_factor = 1
    hash_size = 8
    img_size = hash_size * highfreq_factor

    hash1 = imagehash.phash(Image.open('1_1.jpg'),hash_size=hash_size,highfreq_factor=highfreq_factor)
    print(hash1)
    # > 354adab5054af0b7

    hash2 = imagehash.phash(Image.open('5_1.jpg'),hash_size=hash_size,highfreq_factor=highfreq_factor)
    print(hash2)
    # > 5b7724c8bb364551

    1 - (hash1 - hash2)/len(hash1.hash)**2 # 相似性

difference hashing

梯度散列，计算每个像素的差值，并与平均差异的差异进行比较。

主函数：def dhash(image, hash_size=8)

案例：

1
2
3
4
5
6
7
8
9
10
hash_size = 10
hash1 = imagehash.dhash(Image.open('5_1.jpg'),hash_size=hash_size)
print(hash1)
# > 354adab5054af0b7

hash2 = imagehash.dhash(Image.open('1_1.jpg'),hash_size=hash_size)
print(hash2)
# > 5b7724c8bb364551

1 - (hash1 - hash2)/len(hash1.hash)**2 # 相似性
wavelet hashing

离散小波变换（DWT）是频表示的另一种形式。流行的DCT和傅立叶变换使用余弦函数作为sin\cos的基础：sin(x)，sin(2x)，sin(3x)等等。与此相反，DWT使用一个单一的功能作为基础，但在不同的形式：缩放和移动。基础功能是可以改变的，这就是为什么我们可以有Haar小波，Daubechie-4小波等，这尺度效应给我们很大“时频表示”的时候，低频部分类似于原始信号。

它的工作原理在频域中作为pHash但它使用DWT代替DCT变换。
主函数：def whash(image, hash_size = 8, image_scale = None, mode = ‘haar’, remove_max_haar_ll = True)

参数：

  • mode:
    ‘haar’ - Haar wavelets, by default
    ‘db4’ - Daubechies wavelets
  • remove_max_haar_ll:是否去掉低频段位，low level (LL) frequency
  • image_scale:图像重新resize成多大，一定是2的倍数

案例：

1
2
3
4
5
6
7
8
9
10
11
12
hash_size = 8
mode = 'db4'
image_scale = 64
hash1 = imagehash.whash(Image.open('1_1.jpg'),image_scale=image_scale,hash_size=hash_size,mode = mode)
print(hash1)
# > 354adab5054af0b7

hash2 = imagehash.whash(Image.open('5_1.jpg'),image_scale=image_scale,hash_size=hash_size,mode = mode)
print(hash2)
# > 5b7724c8bb364551

1 - (hash1 - hash2)/len(hash1.hash)**2 # 相似性

更多代码：https://github.com/bjlhx15/python-algorithm.git

一分也是爱，两分情更浓【还没有人赞赏，支持一下呗】